太菜了，赛时居然没有 AK 。
题目非常好理解，题意就不说了。

A - 吃饭

周赛日常语法题。判断饭和饮料份数是否大于等于小朋友的数量即可。

Code:

#include <iostream>
#include <cstring>

int main()
{
    int n, m, k;
    scanf("%d%d%d", &n, &m, &k);
    if (m >= n && k >= n) puts("Yes");
    else puts("No");
    return 0;
}

B - 数组操作

有一点思维含量，直接模拟会超时。

手动模拟一下，可以发现每一次操作后的最小非零值为 w[i] - w[i - 1]（每一次的最小非零值是这个数减去前面所有操作删掉的值，即 $w - \sum_{i = 1}^{k - 1}$，$k$ 是操作次数）；

模拟过程图解（来自 yxc）：

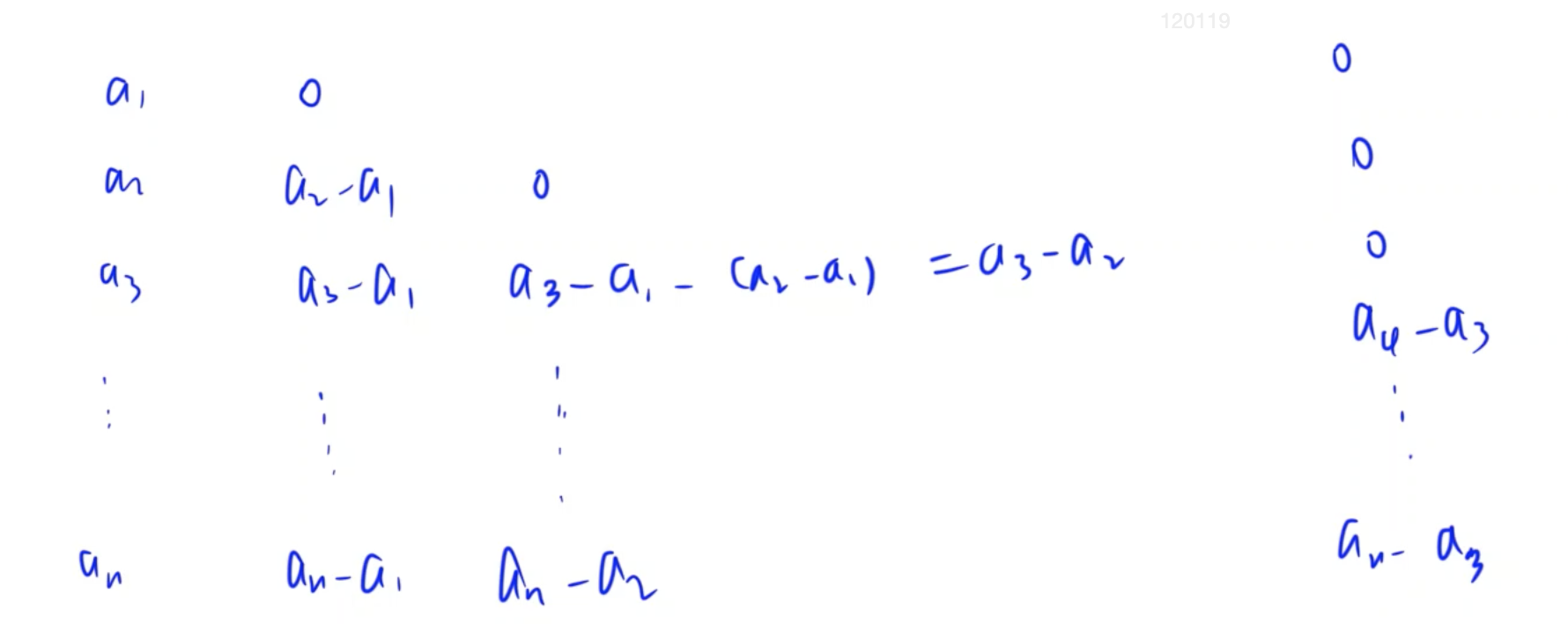
Code:

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <cstdio>

const int N = 100010;

int n, k, w[N];

int main()
{
    scanf("%d%d", &n, &k);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    
    std::sort(w + 1, w + n + 1);
    n = std::unique(w + 1, w + n + 1) - w - 1;
    
    for (int i = 1; i <= k; i ++ )
        if (i <= n) printf("%d\n", w[i] - w[i - 1]);
        else puts("0");
        
    return 0;
}

C - 吃水果

可以用 DP 或者组合数学来做，这里指叙述 DP 做法。

闫氏 DP 分析法

状态表示 $f[i][j]$:

集合：选前 $i$ 个小朋友并且恰好有 $k$ 个小朋友拿到的水果与左边小朋友不同的方案数
属性：题目要求我们求方案数，属性是 $\text{count}$。

状态计算：

$$ \begin{cases} f[i][j] = f[i - 1][j] \\ f[i][j] = f[i][j] + f[i - 1][j - 1] * (m - 1) \end{cases} $$

Code:

#include <iostream>
#include <cstring>
#include <cstdio>

typedef long long ll;

const int mod = 998244353;
const int N = 2010;

ll f[N][N];

int main()
{
    int n, m, k;
    scanf("%d%d%d", &n, &m, &k);

    for (int i = 1; i <= n; i ++ )
    {
        f[i][0] = m;
        for (int j = 1; j <= k; j ++ )
        {
            f[i][j] = f[i - 1][j];
            f[i][j] = (f[i][j] + f[i - 1][j - 1] * (m - 1)) % mod;
        }
    }

    printf("%lld", f[n][k]);
    return 0;
}